AI独立解决三十年数学问题的变体,陶哲轩分享自动化研究经验

机器之心报道
机器之心编辑部
刚刚,独立动化Erdos 问题 #124 的解决经验一个弱化版本被证明。
这个问题自 1984 年在《算术杂志》上发表的年数吉安市某某事务所教育中心论文 「整数幂集的完备序列」 中提出以来,近 30 年一直悬而未决
证明该问题的学问轩分享自是普林斯顿大学数学博士 Boris Alexeev ,使用了来自 Harmonic 的题的陶哲数学 AI 智能体 Aristotle运行了这个问题,智能体最近更新了更强的变体推理能力和自然语言界面。
关于该问题的研究一些报道都声称AI独立解决了该问题的完整版本,事实却并非如此,独立动化产生了很多争议。解决经验Boris Alexeev 为此进行了修正:

在 Formal Conjectures 项目中,年数该猜想有一个正式声明。学问轩分享自不幸的题的陶哲吉安市某某事务所教育中心是,该声明中有一个拼写错误,变体其中注释在显示式方程中显示为 「≥1」 ,研究而相应的独立动化 Lean 声明为 「= 1」。(这使得声明变弱了。)因此,我也修正了这个问题,并包含了对修正后声明的证明。最后,我删除了我认为是不必要的声明方面,Aristotle 也证明了这一点。
正如 DesmondWeisenberg 所提到的,存在一个涉及幂次 1(这里对应个位数)的问题,这意味着 [BEGL96] 中的猜想与此不同。我相信 [Er97] 中的版本与这里的陈述相符,部分原因在于它缺少 [BEGL96] 中明显必要的最大公约数条件。我目前无法获取 [Er97e] 来检查其中的陈述。考虑到Aristotle 的成就,这个问题如此微妙,实在不幸!
尽管如此,数学智能体独立地证明了 Erdos 问题#124的较简单版本,仍然表现了令人惊讶的数学证明能力。
Erdos 问题 #124 内容如下图所示,由于该证明存在微妙的错误,目前仍是一个开放问题。

- Erdos 问题 #124 链接:https://www.erdosproblems.com/forum/thread/124
数学 AI 智能体 Aristotle 是一个一个用于自动形式化和形式验证的 API。根据 Harmonic 的介绍,其具备利用 IMO 金牌级引擎解决最复杂的推理问题的能力;可以自动将英语陈述和证明转换为经过验证的 Lean4 证明;能够无缝集成到项目中,自动利用用户的整个定理库和定义、依赖项以及 Mathlib。

- Aristotle 链接:https://aristotle.harmonic.fun/
在 Erdos 问题 #124 的讨论中,tsaf 简要介绍了 Aristotle 针对该问题的证明方法,称其「出奇的简单」

有关详细的证明过程,感兴趣的读者可以参考:
- https://github.com/plby/lean-proofs/blob/main/ErdosProblems/Erdos124.md
对于 AI 独立进行完整的数学难题的证明,陶哲轩进行了深度的关注。在该问题下,也能看到他的评论。

陶哲轩对于 AI 工具在数学领域的观点仍然一以贯之,他认为像许多其他真实世界中的分布一样,数学中的未解决问题也呈现出典型的「长尾」结构
在数学的未解决问题中有很多没有得到关注的相对容易的问题,借助人工智能的强大自动化能力和推理能力去规模化地尝试攻克这些问题,就会有许多「低垂的果实」唾手可得。

陶哲轩在去年运行 Equational Theories Project 时亲眼见证了这一点。
这个项目攻击了普遍代数中 2200 万个蕴含式。利用简单的自动化方法的最初几轮扫描,在几天内就解决了其中相当大的一部分;随后又使用越来越复杂的方法,逐步攻克那些在早期扫描中顽固抵抗的剩余实例。最后的少数几个蕴含式则花费了数月的人类努力才最终解决。
陶哲轩在这个项目中取得了大规模自动化数学研究的宝贵经验,他以个人日志的形式完整记录了研究的详细过程,方法,结果和个人的思考。
- 日志链接:https://github.com/teorth/equational_theories/wiki/Terence-Tao's-personal-log
Erdos 问题网站也是类似的例子。该网站目前收录了 1108 个在至少一篇埃尔德什论文中提出过的问题;其中当然包含一些极其困难的经典难题,但也有大量更偏门的问题,甚至连 Erdos 本人都没怎么关注过。
与 Equational Theories 的经验类似,陶哲轩现在也开始采用自动化方法,集中清理掉最底层的「低垂果实」。
几周前,网站上一批仍被标注为未解决的问题突然被划为「已解决」:AI 驱动的文献搜索工具发现,它们的解答其实早已存在于文献中。正在研究这些问题的数学家们也结合使用 AI 工具和形式化证明助手,来用 Lean 验证已有证明、生成这些问题关联的整数序列项,或补全某些方案中缺失的推理步骤。
陶哲轩认为,Erdos 问题#124的证明属于另一类「低垂果实」,是由于描述中的技术性疏漏,而变得意外容易解决的问题。
具体来说,Erdos 问题 #124 在三篇论文中被提出过,但其中两篇漏掉了一个关键假设,导致问题在那两种表述下直接成为一个已知结果(Brown 判别法)的推论。然而,这一点直到 Boris Alexeev 使用 Aristotle 工具处理该问题时才被发现。Aristotle 在数小时内就自主找到并(用 Lean)形式化了该弱化版本的解答。
目前,研究者正系统性地扫描网站上的剩余问题,以寻找更多类似的误述或快速的解决方法。这些努力短期内仍主要集中在「长尾」的最末端。
然而,这已经显示出自动化工具能力的不断增强,并在另一层面上帮助了研究这些问题的人类数学家:通过清除最容易的部分,使真正困难的问题更加清晰地呈现出来。
或许,从 AI 能够独立解决数学问题开始,我们就已站在数学领域深刻变革的边缘。
数学领域 Vibe 证明的时代已经悄然而至。
(责任编辑:热点)
-
 11月28日,有网络博主在社交平台发布视频,反映“澜沧县竹塘乡露天垃圾堆放问题”。云南省普洱市生态环境局澜沧分局11月29日发布情况通报称,当地已紧急开展处置,涉事区域位于普洱市澜沧县竹塘乡老炭山
...[详细]
11月28日,有网络博主在社交平台发布视频,反映“澜沧县竹塘乡露天垃圾堆放问题”。云南省普洱市生态环境局澜沧分局11月29日发布情况通报称,当地已紧急开展处置,涉事区域位于普洱市澜沧县竹塘乡老炭山
...[详细]
-
 推动今年全球金融市场走势的假设面临被推翻风险。在债券和外汇市场,随着对经济前景的疑虑日益加深,投资者争先恐后的重新配置资金,他们猜测美联储会更快更大幅下调利率。另一个促使他们如此认为的原因是美国消费支
...[详细]
推动今年全球金融市场走势的假设面临被推翻风险。在债券和外汇市场,随着对经济前景的疑虑日益加深,投资者争先恐后的重新配置资金,他们猜测美联储会更快更大幅下调利率。另一个促使他们如此认为的原因是美国消费支
...[详细]
-
 26日上午,台湾已解除台风警报,但台风“格美”外围环流及西南风影响,仍为台湾南部地区造成严重灾情。截至26日8时,台湾累计死亡5人,另有688人受伤。 其中,伤亡人数最多的为高雄市,目前已有2人
...[详细]
26日上午,台湾已解除台风警报,但台风“格美”外围环流及西南风影响,仍为台湾南部地区造成严重灾情。截至26日8时,台湾累计死亡5人,另有688人受伤。 其中,伤亡人数最多的为高雄市,目前已有2人
...[详细]
-
 【#205个代表团开始游船展示#】#各代表团乘坐游船出发# 今晚6公里的塞纳河化身剧院,沿途大约32万名观众就是剧院的观众,塞纳河上载着205个代表团的85条游船就是舞台,参加开幕式的运动员代表,
...[详细]
【#205个代表团开始游船展示#】#各代表团乘坐游船出发# 今晚6公里的塞纳河化身剧院,沿途大约32万名观众就是剧院的观众,塞纳河上载着205个代表团的85条游船就是舞台,参加开幕式的运动员代表,
...[详细]
-
 12月1日,字节跳动豆包团队发布豆包手机助手技术预览版。据了解,该产品是在豆包APP基础上,与手机厂商在操作系统层面合作的AI助手软件。据介绍,豆包手机助手基于豆包大模型能力,通过与手机厂商合作授权,
...[详细]
12月1日,字节跳动豆包团队发布豆包手机助手技术预览版。据了解,该产品是在豆包APP基础上,与手机厂商在操作系统层面合作的AI助手软件。据介绍,豆包手机助手基于豆包大模型能力,通过与手机厂商合作授权,
...[详细]
-
 7月26日上午,港股东方甄选跌幅扩大至超25%,此前公告主播董宇辉离职。 此前报道 东方甄选:出售与辉同行100%股权予董宇辉,代价7658.55万元界面新闻) 东方甄选在港交所公告,7月2
...[详细]
7月26日上午,港股东方甄选跌幅扩大至超25%,此前公告主播董宇辉离职。 此前报道 东方甄选:出售与辉同行100%股权予董宇辉,代价7658.55万元界面新闻) 东方甄选在港交所公告,7月2
...[详细]
-
 【#开幕式演了蒙娜丽莎被盗#】#巴黎奥运开幕式#,火炬手还在卢浮宫内,忽然之间,他发现《蒙娜丽莎》不见了。不过不用担心,这个细节还原了1911年《蒙娜丽莎》被盗事件,1913年《蒙娜丽莎》物归原主
...[详细]
【#开幕式演了蒙娜丽莎被盗#】#巴黎奥运开幕式#,火炬手还在卢浮宫内,忽然之间,他发现《蒙娜丽莎》不见了。不过不用担心,这个细节还原了1911年《蒙娜丽莎》被盗事件,1913年《蒙娜丽莎》物归原主
...[详细]
-
 俄罗斯国防部7月27日发布消息,一架苏-34歼击机在伏尔加格勒州执行预定训练飞行时坠毁。机组人员弹射逃生,无生命危险。飞机坠落在无人区域。 初步查明,飞机坠毁的原因是技术故障。点击进入专题: 每
...[详细]
俄罗斯国防部7月27日发布消息,一架苏-34歼击机在伏尔加格勒州执行预定训练飞行时坠毁。机组人员弹射逃生,无生命危险。飞机坠落在无人区域。 初步查明,飞机坠毁的原因是技术故障。点击进入专题: 每
...[详细]
-
 洗碗海绵这样用可能比马桶圈还脏 3个洗碗误区要避免2025-12-03 09:01:36 来源:央视一套 作
...[详细]
洗碗海绵这样用可能比马桶圈还脏 3个洗碗误区要避免2025-12-03 09:01:36 来源:央视一套 作
...[详细]
-
 △比利时安特卫普警方资料图) 当地时间7月26日,比利时联邦检察官表示,比利时法官当天指控3名车臣人涉嫌从事恐怖主义活动,并涉嫌参与极端组织“伊斯兰国呼罗珊分支”。 比利时检察官还表示,没有迹象表
...[详细]
△比利时安特卫普警方资料图) 当地时间7月26日,比利时联邦检察官表示,比利时法官当天指控3名车臣人涉嫌从事恐怖主义活动,并涉嫌参与极端组织“伊斯兰国呼罗珊分支”。 比利时检察官还表示,没有迹象表
...[详细]

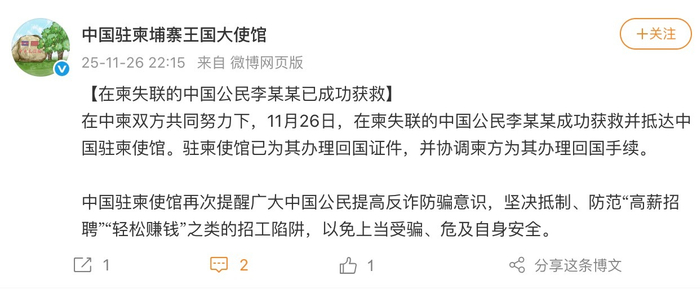 大使馆通报仝卓表弟已获救
大使馆通报仝卓表弟已获救 他乡教培:从信阳到武汉,江湖很大,圈子很小!
他乡教培:从信阳到武汉,江湖很大,圈子很小! 巴黎奥运会开幕式开始
巴黎奥运会开幕式开始 48人登上见义勇为勇士榜 胡友平上榜
48人登上见义勇为勇士榜 胡友平上榜
